Steady-State Concentration: Principles, Calculations, and Clinical Application

Steady state is a cornerstone concept in clinical pharmacokinetics. It connects dose, dosing interval, and patient-specific clearance to the drug concentrations that drive therapeutic and adverse effects. Yet, “steady state” is often misunderstood or oversimplified. This chapter explains what steady state is (and is not), how it arises under different dosing schemes, how to calculate and predict steady-state concentrations, and how to apply these ideas to individualized dosing and therapeutic drug monitoring (TDM). We highlight linear versus nonlinear behavior, infusion versus intermittent dosing, accumulation, fluctuation, loading doses, and special scenarios such as long-acting formulations, critical illness, and altered protein binding.

Key takeaways

Definition

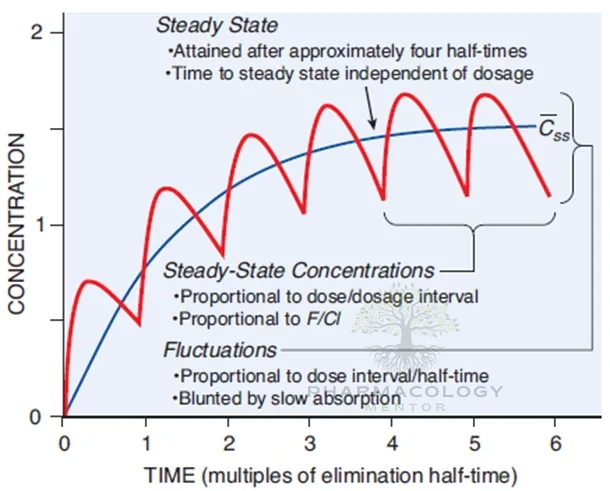
Steady state exists when, under time-invariant conditions, the concentration–time profile repeats identically during each dosing interval. Fundamentally, this means drug input equals drug elimination over each cycle [1–3].

Mathematical Formulas (Linear Kinetics)

For linear kinetics, the average steady-state concentration (C_ss,avg) depends only on the dose rate and clearance (CL).

Key Kinetic Principles

• Time to Steady State: This is determined solely by the elimination half-life (t_1/2), not the dose. It takes approximately 4–5 half-lives to approach >90–97% of steady state [1–3].
• Accumulation and Fluctuation: These are governed by the relationship between the dosing interval (τ) and the half-life. A longer τ typically increases peak–trough variation [1,3,4].
• Nonlinear Kinetics: Factors such as saturation or autoinduction (time-varying kinetics) will shift the steady state, invalidating simple linear predictions [1,2].

Clinical Application

• Sampling: When using concentration targets, samples should be drawn at or near steady state.
• Protein Binding: Consider unbound drug concentrations if protein binding is altered (e.g., hypoalbuminemia) [3,5].

Defining Steady State

What steady state means

Steady state is achieved during multiple dosing or continuous infusion when the amount of drug entering the body per unit time equals the amount eliminated per unit time, given constant pharmacokinetic parameters (clearance, volume, bioavailability). At that point, concentrations over each dosing interval repeat in a stable pattern: same peak, trough, and area under the curve (AUC) each cycle [1–3].

Important nuances:

• Steady state is a dynamic equilibrium: continuous input and elimination, not stasis.
• It refers to the entire periodic concentration–time profile, not a single number (unless infusion, where concentration becomes constant after sufficient time).
• It requires time-invariant PK; if clearance or bioavailability changes (enzyme induction, organ failure), the steady state shifts [1,2].

Distinguishing average, peak, and trough at steady state

• Css,avg (average over a dosing interval) is the primary exposure metric linking dose rate and clearance.
• Cmax,ss and Cmin,ss are the steady-state peak and trough; they depend on both clearance and the dosing interval relative to half-life (fluctuation) and on absorption rate for extravascular dosing [1–3].

Mathematical Foundations

Linear kinetics and superposition

For most dose ranges, many drugs follow linear (first-order) kinetics: pharmacokinetic parameters are constant, and exposure (AUC) is proportional to dose. Multiple dosing and infusion can be handled using superposition: the total concentration is the sum of individual single-dose contributions shifted by integer multiples of the dosing interval [1–3].

Key Linear Pharmacokinetic Relations

Fundamental Equations

Time to Steady State

The time required to reach steady state depends only on the elimination half-life (t_1/2).

• 1 half-life: 50% reached
• 2 half-lives: 75% reached
• 3 half-lives: ~87.5% reached
• 4 half-lives: ~94% reached
• 5 half-lives: ~97% reached

General Rule: It typically takes 4 to 5 half-lives to reach clinical steady state.

Accumulation Ratio (R_acc)

For intermittent dosing in a one-compartment model:

Fluctuation at Steady State

Fluctuation is the ratio of peak to trough within a dosing interval. For one-compartment IV bolus dosing:

Thus, for a given half-life, shortening the dosing interval reduces fluctuation (more even concentrations), while lengthening it increases fluctuation [1–3].

Steady State Under Different Dosing Schemes

A. Continuous IV Infusion

• Concentration: C(t) = C_ss × [1 − e^{−k × t}] (where C_ss = R₀/CL).
• Stopping infusion: Leads to a mono-exponential decline: C(t) = C_ss × e^{−k × t}.
• Clinical Strategy: Use a loading dose to reach C_ss rapidly. Infusions enable tight control for narrow therapeutic index drugs with short half-lives (e.g., anesthetics) [1,2].

B. Intermittent IV Bolus

After stabilization, the peak (post-dose) and trough (pre-dose) repeat. For a one-compartment model with immediate distribution:

Caveat: In multicompartment kinetics, “peak” sampling too early may reflect distribution phases and overestimate exposure [1,2].

C. Repeated Oral Dosing

• Linear Validity: C_ss,avg formula remains valid.
• Absorption Rate (k_a): Rapid absorption (k_a >> k) yields sharper peaks/higher fluctuation. Slower absorption smooths the profile.
• Flip-Flop Kinetics: If k_a < k, the terminal slope reflects absorption rather than elimination. Apparent half-life becomes absorption-limited (common in depot/extended-release formulations) [2,3].

Loading Doses and Maintenance

Why Load?

Without a loading dose, it takes ~4–5 half-lives to approach therapeutic levels—too slow for urgent indications (e.g., status epilepticus, sepsis).

Calculations

Note: V should reflect the apparent volume relevant to the target (V_ss). If protein binding is saturable (e.g., valproate), target unbound concentrations [5].

Nonlinear and Time-Dependent Kinetics

Saturation (Capacity-Limited)

• Michaelis–Menten (e.g., Phenytoin): Clearance decreases as concentrations rise. Small dose increases cause disproportionate concentration jumps. Simple linear predictions fail.
• Saturable Binding (e.g., Valproate): Unbound fraction increases with concentration, altering distribution and clearance [2,5].

Time-Dependent Clearance

• Autoinduction (e.g., Carbamazepine): Clearance increases over weeks; concentrations decline unless dose is increased.
• Inhibition: Mechanism-based inhibition decreases clearance until enzymes resynthesize [2].

Unbound Concentrations and Regimen Design

Protein Binding

Pharmacologic effect and clearance are driven by unbound drug (C_ss,u,avg = f_u × C_ss,avg). In conditions like hypoalbuminemia (critical illness), measure free levels for narrow-index drugs [5].

Designing Regimens (Interval τ)

• Trade-offs: Short τ = lower fluctuation but higher burden. Long τ = high fluctuation.
• Time-Dependent Killers (e.g., Beta-lactams): Efficacy requires time > MIC. Use short τ or continuous infusion.
• Concentration-Dependent (e.g., Aminoglycosides): Efficacy driven by Peak/MIC or AUC/MIC. Allow fluctuation to maximize peaks and minimize troughs (toxicity) [6–8].

TDM, Special Situations, and Workflow

Therapeutic Drug Monitoring (TDM)

• Timing: Sample at steady state (unless assessing toxicity/loading).
• Targets: Troughs for immunosuppressants; Timed pairs for Bayesian AUC (Vancomycin); Peaks/Troughs for Aminoglycosides.
• Bayesian Forecasting: Combines population priors with patient data to optimize individual dosage [10,12].

Special Populations

• Augmented Renal Clearance (ARC): ICU patients may have high CL, reducing C_ss,avg.
• Renal Impairment: Reduce dose rate or extend τ proportional to CL reduction.
• Missed Doses: Trough falls by factor e^−kτ. If critical (e.g., transplant), counsel strictly on adherence [2,15].

Worked Logic Checklist

1. Define Target: C_ss,avg, AUC/MIC, or Trough.
2. Estimate Parameters: CL and V from population data.
3. Calculate Dose: Dose Rate = CL × Target.
4. Select Interval (τ): Balance half-life and fluctuation limits.
5. Load if Urgent: LD = Target × V.
6. Verify: TDM at steady state.

Short Clinical Examples

• Vancomycin: Target AUC₂₄/MIC 400–600 mg·h/L. Start with LD (25–30 mg/kg). Use Bayesian monitoring.
• Aminoglycosides: High C_max/MIC favored. Long τ allows low troughs to minimize toxicity.
• Phenytoin: Nonlinear elimination. Use small dose adjustments and measure free concentrations if albumin is low [1,2,5].

Conclusion

Steady state is the kinetic equilibrium that links dose rate to exposure and, ultimately, clinical response. Under linear, time-invariant conditions, its logic is simple: average exposure equals dose rate divided by clearance; half-life dictates how quickly steady state is reached and how much concentrations fluctuate between doses. Real patients add complexity—nonlinear or time-dependent processes, variable protein binding, organ dysfunction, critical illness, and adherence—all of which can shift steady state or complicate its attainment. A disciplined approach—clear exposure targets, rational interval selection, thoughtful use of loading doses, and verification with appropriately timed TDM, ideally via Bayesian methods—translates steady-state theory into safer, more effective therapy.

References

1. Rowland M, Tozer TN, Derendorf H, Hochhaus G. Clinical Pharmacokinetics and Pharmacodynamics: Concepts and Applications. 5th ed. Philadelphia (PA): Wolters Kluwer; 2019.
2. Shargel L, Wu-Pong S, Yu ABC. Applied Biopharmaceutics & Pharmacokinetics. 7th ed. New York (NY): McGraw-Hill; 2015.
3. Gabrielsson J, Weiner D. Pharmacokinetic and Pharmacodynamic Data Analysis: Concepts and Applications. 5th ed. Stockholm (SE): Swedish Pharmaceutical Press; 2016.
4. Benet LZ, Kroetz DL, Sheiner LB. Pharmacokinetics: The Dynamics of Drug Absorption, Distribution, and Elimination. In: Hardman JG, Limbird LE, Goodman Gilman A, editors. Goodman & Gilman’s The Pharmacological Basis of Therapeutics. 9th ed. New York (NY): McGraw-Hill; 1996. p. 3-27.
5. Benet LZ, Hoener BA. Changes in Plasma Protein Binding Have Little Clinical Relevance. Clin Pharmacol Ther. 2002;71(3):115-121.
6. Craig WA. Pharmacokinetic/Pharmacodynamic Parameters: Rationale for Antibacterial Dosing of Mice and Men. Clin Infect Dis. 1998;26(1):1-10.
7. Mouton JW, Brown DFJ, Apfalter P, et al. The Role of Pharmacokinetics/Pharmacodynamics in Setting Clinical MIC Breakpoints: The EUCAST Approach. Clin Microbiol Infect. 2012;18(3):E37-E45.
8. Drusano GL. Antimicrobial Pharmacodynamics: Critical Interactions of ‘Bug and Drug’. Nat Rev Microbiol. 2004;2(4):289-300.
9. Holford NHG, Sheiner LB. Understanding the Dose–Effect Relationship: Clinical Application of Pharmacokinetic–Pharmacodynamic Models. Clin Pharmacokinet. 1981;6(6):429-453.
10. Rybak MJ, Le J, Lodise TP, et al. Therapeutic Monitoring of Vancomycin for Serious Methicillin-Resistant Staphylococcus aureus Infections: A Revised Consensus Guideline and Review by ASHP/PIDS/SIDP/IDSA. Am J Health Syst Pharm. 2020;77(11):835-864.
11. Nicolau DP. Pharmacodynamic Optimization of Beta-Lactams in the Patient Care Setting. Crit Care. 2008;12(Suppl 4):S2.
12. Neely MN, van Guilder MG, Yamada WM, et al. Accurately Achieving Target Concentrations in Children Through Individualized Dosing of Vancomycin. Ther Drug Monit. 2014;36(1):73-80.
13. Udy AA, Roberts JA, Lipman J. Implications of Augmented Renal Clearance in Critically Ill Patients. Nat Rev Nephrol. 2011;7(9):539-543.
14. Roberts JA, Abdul-Aziz MH, Lipman J, et al. Individualised Antibiotic Dosing for Patients Who Are Critically Ill: Challenges and Potential Solutions. Lancet Infect Dis. 2014;14(6):498-509.
15. Vrijens B, De Geest S, Hughes DA, et al. A New Taxonomy for Describing and Defining Adherence to Medications. Br J Clin Pharmacol. 2012;73(5):691-705.